Weyl and Dirac Semimetal

What happen if we close the gal of a 3D topological insulator (TI)?

Then both bulk and surafce behave as a metal !!

Ok. there is something important about TIs is bulk bundary correspondence. Because of the bulk gap the 2D surface states with Dirac cone like dispersion are protected.  So in Z2 TIs the the time and space reversal symmetry  are conserved as roposed by Kane and Male (PRL 2005). Once we close the gap in bulk the these symmetry are broken !! Cane and male theory beak down and they can't be applied anymore. Now the question is , are the topological surface states still exist? 

Yes they do exist !! Now they are protected by crystal symmetry rather than the band topology.

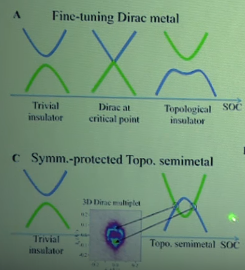
So for trivial insulator the  highest occupied band and lowest empty band are separated by a gap. If SOC coupling is there then  there will be band inversion along with surface states, is a topological insulator. Now these are the two extreme cases. There is another case where, for a Ti the bulk band are just touched each other as similar in graphene. Then these staes is called dirac semimetal where the bulk as well as surface states are Dirac cone like.

Now in the previous case the bulk band touched in sigle point what if, these band crossed each other (Fig. B  above) and there will be two Dirac points along with the surface states , these are called Weyl semimetal. 

So if we measure the dispersion relation (Kz component: momentum perpendicular to surface) of a Dirac or weyl semimetal then both bulk and surface will show Dirac cone. NOw for topological insulator the Dirac cone was only for the suraface states not for the Bulk. So fora weyl semimetal  such measurement will show a single Dirac point at the surface but as soon as we go to the bulk this single point will disperse into two points.

So for topological insulator we have helical Dirac fermion ar the surface which is time and space reversely protected. Now by braking this symmetry we split the  the helical fermion (Fig d bottom) at the surface into  pair of  weyl (Fig.c bottom).

https://www.nature.com/articles/ncomms8373

Hence now the Fermi surface is fractionalised. Now we can"t do that, there should be some way out to complete the loop  with the other channel via bulk (fig.c top) and that's where the bulk come and make it semi-metal. 

  Hence for a Weyl semi-metal we will have a co propagating Fermi arcs of the two separated Weyl points. So if we considr dispersion relation of a weyl semimetal then we will have a copropagating fermi arcs at the surface and well points at the bulk. 

So if we measure bulk Fermi surface we will see a dot instead of a Fermi surface which is common fro insulators. So in ARPES experiment we will see a non closed co-propagating Fermi arcs/ FRACTIONAL FERMI SURFACE (at boundary , low photon energy) and they will terminate at bulk in weyl points (high photon energy measurement).

Experiment by Hasan group from Princeton:

http://science.sciencemag.org/content/349/6248/613

Ok now the idea of Weyl semimetal is established. Let's push ourself  a bit more: For 3D topological insulator we have 2D surface metallic and bulk insulator. Now  Weyl semimetal is a 3D metllic topologically where is the bulk insulated part? We can imagine from the analogy of 3D TIs that as if weyl semimetal is 3D metalic state of a 4D TIs. Ahh this is exciting we are going of higher dimension like string theory.