Thursday, December 28, 2017

Type II Dirac Fermion

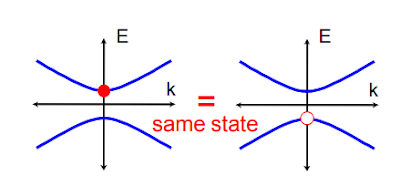
The standard model of particle physics describes all the known elementary particles, like electrons and quarks. Many of these particles have analogs in condensed matter, where they arise as collective states, or quasiparticles. One example is an electronic state in graphene that behaves like a massless Dirac fermion—a spin-1/2 particle that is not its own antiparticle. But condensed-matter physics may offer a longer list of “elementary particles” than found in the standard model. This is due to the fact that—unlike fundamental particles—quasiparticles in solids are not constrained by so-called Lorentz invariance. A Lorentz-violating quasiparticle is one whose momentum-energy relation depends on the direction it travels. Three separate teams have collected the first experimental evidence of quasiparticles called type-II Dirac fermions, which break Lorentz invariance. These electronic states, which have no counterpart in the standard model, could be associated with a new type of superconductivity, which has potential applications in thermoelectric devices and quantum computing.

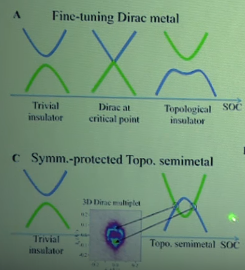
For type-I Dirac [and Weyl semimetals which obey Lorentz invariance, massless Dirac fermions with linear dispersions are expected at the Dirac or Weyl points. Type-II Dirac and Weyl fermions emerge at the topologically protected touching points of electron and hole pockets, and they show highly tilted Dirac cones along certain momentum direction (see schematics bottom figure), thereby breaking the Lorentz invariance . The anisotropic electronic structure can also lead to anisotropic MR, and negative MR is expected only along directions where the cones are not tilted enough to break the Lorentz invariance . Type-II Dirac semimetal can be tuned to a Weyl semimetal or topological crystalline insulator when the crystal symmetry or time reversal symmetry is broken , and therefore they are ideal candidates for investigating topological phase transitions and potential device applications.

Materials: PtTe2, PtSe2,,PdTe2,

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.119.016401

https://arxiv.org/abs/1607.03643

https://journals.aps.org/prb/abstract/10.1103/PhysRevB.96.041201

https://journals.aps.org/prb/abstract/10.1103/PhysRevB.95.155112

website:
http://nccr-marvel.ch/fr/news/highlights/2017-07-typeII-dirac-fermions-now-experimetally-verified

Topological Magnon Insulator

The dispersion relations of magnons in ferromagnetic pyrochlores with Dzyaloshinskii-Moriya interaction are shown to possess all types of topologically protected states:.

The breakthrough experiment that lead to such state is observation of Magnon hall effect .

Edge states in topological magnon insulators

Weyl magnons in breathing pyrochlore antiferromagnets

Topological magnon insulator in insulating ferromagnet

Magnon nodal-line semimetals and drumhead surface states in anisotropic pyrochlore ferromagnets

Weyl and Nodal Ring Magnons in Three-Dimensional Honeycomb Lattices

Monday, December 25, 2017

Topological Superconductor

Particle hole symmetry is one of the remarkable conclusion of BCS theory.Superconductor similar to insulator in the the sense they have energy gap between the quasiparticle excitation. Now for superconductor there is intrinsic symmetry that valence and conduction are exactly mirror image of each other. But for insulator those are different. Adding an electron in conduction band is equivalent to electron from valence bond. Now for insulator these two case are independent as the valence and conduction band are independent of each other. In superconductor these states are actually same states !! In case of superconductor, For superconductor creating an particle at +E and destroying a particle at -E are in same state. This known as particle hole symmetry.

Now a question is , Does a Hamiltonian (antiunitary) that satisfy particle hole symmetry have a topological class. If yes then that would be a topological superconductor !!

In 1D there is possibility of Z2 topological superconductor. These Topological superconductor end host Majorana fermions at the edge with zero mode.

In 2D, we will have chiral majorana edge states which are protected as integer quantum hall state. But here because of particle hole symmetry the chiral state with positive and negative are redundant

here time reversal symmetry is broken and it ins Z(n) topological insulator as any integer number (n) of chiral state are possible not Z2 as in case of 1D .It is possible to observe majorana zero mode at the vortex of 2D topological superconductor.

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.100.096407

https://www.nature.com/articles/nphys3036

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.103.107002

https://www.nature.com/articles/nmat3255

possible topological superconductivity in

{Sn}_{1 - x} {In}_{x} Te

${Cu}_{x} {Bi}_{2} {Se}_{3} theory$

$Superconductivity in {Cu}_{x} {Bi}_{2} {Se}_{3} Expt$

Now what about 3D. from the following periodic table

By Kiataev and in PRB

Classification of topological insulators and superconductors in three spatial dimensions

Classification of topological quantum matter with symmetries

The DIII could host a 3D topological superconductor.The quasiparticles on the surface of a 3D topological insulator are massless Dirac fermions, familiar from graphene. The superconducting counterpart has massless Majorana fermions on its surface

The Majorana Fermions

Story start with discovery of antiparticle (Positron) by Dirac by an attempt to unified Theory of relativity and Quantum mechanics. 1932 positron was discovered in 192 in cosmic ray. Dirac equation describe charged spin 1/2 Fermions.
In 1937 Majorana predicted one new type of perticle by smartly choosing gamma matrices of Diraction so that the wave function of the particle is real and then this particle will be self conjugate. But don't forgate it is still a spin 1/2 Fermion !! Waoo.. that.s amazing a charge neutral, spin1/2, self conjugate (a particle with it's own anti particle) Fermion.

In condensed matter there is findings of Majorana Bound state on the boundary of a 1D topological supercoductor (0+1) that are localize not propagating

Edge of a 1D superconductor :

https://arxiv.org/abs/cond-mat/0010440

If in a 1D wire,in the middle there is no state but there is at the end. Now if it has a state in positive side then it should have it’s partner in negative side. But this not true for the is zero energy state at the end and it don’t have any partner. Now this state we can’t get rid of it.It is topologically protected. If we try to move it away then the partner could be nowhere to be found. Now adding a particle in this zero energy state is equivalent to removing the same from this zero energy state!! So this zero energy particle is it’s antiparticle means it’s half of it’s particle. Called Majorana particle.

Sunday, December 24, 2017

Topological Crystalline Insulator (TCI)

Unlike Z2 class of topological insulator where the states are protected by TR and SI symmetry. InTCI it is the crystal symmetry that protect it. Time-reversal symmetry protects strong topological insulators of the Z2 class, which possess an odd number of metallic surface states with dispersion of a Dirac cone. Topological crystalline insulators are merely protected by individual crystal symmetries and exist for an even number of Dirac cones. Here we mirror chern number.

SnTe is an example where the band inversion is protected by mirror symmetry but it is not the case for PbTe

In thus case te surface states Dirac cone neither is at corner of Brilouin Zone (Z2 TI) or in the symetry axis (Dirac semimetal) rather it is situated on mirror inversion point. inset of bottom of figure.

Unlike Graphene these Dirac point can"t annihilate. So what is the difference between TI and TCI ?

In TI there are odd no of Dirac cone situated on time reversal point in momentum space but for TCI there are even no of Dirac cone which are situated any where except the time reversal point.

Now one interesting point is if we break the mirror inversion symmetry then a gap will appear in Dirac cone which will lead to appearance of mass. This symmetry can be broken by structural distortion upon lowering the temperature. There is a report here

http://science.sciencemag.org/content/341/6153/1496

===============================================================================================================================================

Prediction by a toy model (2010) https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.106.106802

https://www.nature.com/articles/ncomms1969

SnTe (2012): https://www.nature.com/articles/nphys2442

https://www.nature.com/articles/nmat3449

https://www.nature.com/articles/ncomms2191

Observation of ferroelectricity and proposal of ferroelectric tunneling random access memory.!!

http://science.sciencemag.org/content/353/6296/274

A complete review by Liang Fu;

http://www.annualreviews.org/doi/10.1146/annurev-conmatphys-031214-014501

This paper demonstrate between Z2 to TCI: https://www.nature.com/articles/s41467-017-01204-0

Further Idea:

Hourglass fermions :https://www.nature.com/articles/nature17410

Non symorphic TI: https://journals.aps.org/prb/references/10.1103/PhysRevB.96.165143

One point to remember upto now we have not consider any interaction in TCI !!

Dirac Semimetal

Dirac semimetal are 3D versions of 2D graphene. In case of Graphene the Dirac point are only in the corner of hexagonal Briloune Zone which are time and space reversely protected. In Dirac semimetal, these Dirac points are now inside the Brilouine Zone along the symmetry axis.

Grphene Dirac cone

Dirac semimetal Dirac cone

This happen by considering the point group symmetry along with Time reversal and space inversion symmetry..PHYSICAL REVIEW B 85, 195320 a material prediction in Na3Bi in the year 2012.

In Na3Bi there is band crossing because of spin orbit interaction at K_D and there is other one also at -K_D. Now such crossing are protected against gap formation by point group symmetry as they they different representation they can"t never hybridize.

Na3Bi has C3 point group symmetry (http://science.sciencemag.org/content/343/6173/864/tab-pdf)

Cd3As2 has C4 symmetry (https://www.nature.com/articles/nmat3990

https://www.nature.com/articles/ncomms4786

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.113.027603

)

As already discussed if we broke either time reversal (by applying magnetic field or having a spontaneous magnetization ) or space inversion the we will get Wyel semimetal. As theoriticaly predicted in 2011 by Vishwanath

https://journals.aps.org/prb/abstract/10.1103/PhysRevB.83.205101

Weyl found an important conclusion of Dirac equation:

1>Start with Durac equtaion and set the mass zero

2?Do not include any electromagnetic interaction

Then we have a mass less Dirac Fermion with two different population of opposite chirality and they never mixed up. When there is mass term then this two chirality will mixed up.

In 2D this equivalent to parity. So let's talk about chirality in more details:

Weyl and Dirac Semimetal

What happen if we close the gal of a 3D topological insulator (TI)?

Then both bulk and surafce behave as a metal !!

Ok. there is something important about TIs is bulk bundary correspondence. Because of the bulk gap the 2D surface states with Dirac cone like dispersion are protected. So in Z2 TIs the the time and space reversal symmetry are conserved as roposed by Kane and Male (PRL 2005). Once we close the gap in bulk the these symmetry are broken !! Cane and male theory beak down and they can't be applied anymore. Now the question is , are the topological surface states still exist?

Yes they do exist !! Now they are protected by crystal symmetry rather than the band topology.

So for trivial insulator the highest occupied band and lowest empty band are separated by a gap. If SOC coupling is there then there will be band inversion along with surface states, is a topological insulator. Now these are the two extreme cases. There is another case where, for a Ti the bulk band are just touched each other as similar in graphene. Then these staes is called dirac semimetal where the bulk as well as surface states are Dirac cone like.

Now in the previous case the bulk band touched in sigle point what if, these band crossed each other (Fig. B above) and there will be two Dirac points along with the surface states , these are called Weyl semimetal.

So if we measure the dispersion relation (Kz component: momentum perpendicular to surface) of a Dirac or weyl semimetal then both bulk and surface will show Dirac cone. NOw for topological insulator the Dirac cone was only for the suraface states not for the Bulk. So fora weyl semimetal such measurement will show a single Dirac point at the surface but as soon as we go to the bulk this single point will disperse into two points.

So for topological insulator we have helical Dirac fermion ar the surface which is time and space reversely protected. Now by braking this symmetry we split the the helical fermion (Fig d bottom) at the surface into pair of weyl (Fig.c bottom).

https://www.nature.com/articles/ncomms8373

Hence now the Fermi surface is fractionalised. Now we can"t do that, there should be some way out to complete the loop with the other channel via bulk (fig.c top) and that's where the bulk come and make it semi-metal.

Hence for a Weyl semi-metal we will have a co propagating Fermi arcs of the two separated Weyl points. So if we considr dispersion relation of a weyl semimetal then we will have a copropagating fermi arcs at the surface and well points at the bulk.

So if we measure bulk Fermi surface we will see a dot instead of a Fermi surface which is common fro insulators. So in ARPES experiment we will see a non closed co-propagating Fermi arcs/ FRACTIONAL FERMI SURFACE (at boundary , low photon energy) and they will terminate at bulk in weyl points (high photon energy measurement).

Experiment by Hasan group from Princeton:

http://science.sciencemag.org/content/349/6248/613

Ok now the idea of Weyl semimetal is established. Let's push ourself a bit more: For 3D topological insulator we have 2D surface metallic and bulk insulator. Now Weyl semimetal is a 3D metllic topologically where is the bulk insulated part? We can imagine from the analogy of 3D TIs that as if weyl semimetal is 3D metalic state of a 4D TIs. Ahh this is exciting we are going of higher dimension like string theory.

Saturday, December 23, 2017

Different types of Available topological insulator till date

Upto now there are there types of available Topological insulator :

1> The chern Insulator : 2D free electron gas under magnetic field. The integar and fractional quantum hall effct. The chen number is basically the TKNN invariant of occupied band.

2> Z2 Type: As predicted by Cane ad Mele the time reversal invariant topological insulator.

3> Topological crystalline insulator: proposed by Liang Fu PRL 106, 106802 (2011) here the richness and beauty of the crystal symmetry drives the topological nature

Experiment: http://science.sciencemag.org/content/341/6153/1496

One of the common thing among this three class is that they all have non vanishing Berry Curvature !

Now there is this paper predicting a NEW TOPOLOGICAL class without Bery Curvature but Berry connection.

3D (Topological Insulator) version of 2D fractional quantum hall effect

The fractional quantum hall effect observed in 2D system is one of the remarkable result of topological nature of band. Now one much more awaiting phenomenon is to observation 3D version of 2D fractional Quantum hall effect. For integer quantum hall effect (observed in 2D electron gas under magnetic field) the time reversal protected chiral edge state are in 1D. Now a 3D topological insulator where we have chiral edge states in 2D (as similar Graphene, but in Graphene everything occur from band theory whereas in topological insulator it's the symmetry protected surface topological states ). In this analogy, 3D topological insulator can be thought as a dimensional extension of 2D integar quantum hall effect.

Similarly, one would expect to a 3D (Topological Insulator) version of 2D fractional quantum hall effect !! Waooo that would much more interesting from because the excitation in that system will be just extraordinary !! As in 2D (http://www.tandfonline.com/doi/abs/10.1080/00018739500101566) fractional quantum hall effect electron electron correlation played a crucial role (which not the case for integer quantum hall effect) , on have consider similar interaction in 3D topological insulator.

There is a proposal of this here
https://journals.aps.org/prb/abstract/10.1103/PhysRevB.96.085422

Thursday, December 21, 2017

Realization of quantum anomalous Hall effect from a magnetic Weyl semimetal

The following article predicted observation of quantum anomalous hall effect in Wyel semimetal. So far, there are already many candidates for the magnetic WSMs from theoretical proposals, and some of them host strong AHE. Now quantum anomalous hall effect is observed in 2D insulating system having chiral edeg state whereas wyel semimetal is 3D topological system (sort of metalic). They proposed that Co3Sn2S2 is a promising candidate by breaking translational symmetry along one direction of low carrier density Wyel semimetal.

https://arxiv.org/abs/1712.08115

Sunday, December 17, 2017

3D topological insulator

If we stack quantum hall insulator on upon other then we will get current only in the edge but this does not give rise a edge current on to and bottom of this state. Now for 3D topological hall insulator what we want is edge state driven current through the 2D surface state of a 3D bulk. So what we want is following:

For 2D topological insulator, edge state formed a cross sign "X"by up and down spin, for 3D topological insulator we want them to form cone, the 3D vrsion of the "Cross X " . So i am talking is a Dirac cone.

Bi based materials:
Bi has strong spin orbit coupling. If we take Bi-n, Bi-As then because of Rashba coupling give a pair of Fermi surface with up down spin at the surface. These are pair of Rashba states by breaking the time reversal symmetry at surface.
Now for Bi2Se3, Bi-Sb the situtaion is different, we have only one Fermi surface and in momentum space the K+ ,K- has opposite spin. As shown in following figure z axis is energy and x,y axis are momentum. If we cut the circle formed by the top of cone, the spin momentum has always opposite sign.So the spin form a clockwise spin texture at the top of the cone. Now if go towards center point of the cone the this opposite nature of spin is maintained. It has half the degree of freedom compare to Rashba system. So at he end the surface is gapless

Now this type band dispersion is exist only in the surface not for the bulk. Because such dispersion of energy(E) moment(k_x, k_y) is studied by doing ARPES at the surface of Bi2Se3. In order to make sure that it exist only at the surface not in the bulk, a K_z dependent study is needed. Now a K_z study revealed that the surface edge states , lates call them now Dirac band are non dispersive as function of K_z where as the bulk band is dispersive.

So the surface state contain, K_+ has spin polarization has up and K_ - has spin down. So this surface state has half the degree of freedom than the Rashba system. Remember the whole system is nonmagnetic. Now the Dirac cone make sure that back scattering is not allowed. The surface electron has spin momentum lock. These are called helical Fermion.

Now what is the fundamental difference between the normal insulator and such surface states with metallic state and bulk being insulator.

In the above figure one of Selenium site has been substituted by lower Z value atom salphar to decrease spin orbit coupling. The extreme the bulk and surface is also insulator. So this is spin orbit coupled Bloch band insulator. In the right side there is formation of surface state provided the bulk band has closed the gap at 0.6. So there is phase transition , only odd number of band inversion has happen in he bulk then only surface states appear.

Saturday, December 16, 2017

Quantum hall effect without magnetic field

For quantum hall effect the interior of the material does not carry a current.The electron have full circular motion and has net contribution is zero. Rather the boundary has skipping orbits of electron and carry current. Now this current can flow in one direction.This is classical analogue.

In quantum mechanics these are expressed as edge state connecting between valance and conduction band (Phys. Rev. B 25, 2185). These are edge states are call called chiral edge state which are topologically protected. Now in this edge state electric current flow without dissipation. In IQH measurement we measure the transport of this chiral edge state. Now this does not depend on the edge of the sample, geometry etc. But this edge state are entirely determine by the bulk bands So this is called bulk-boundary correspondence. Unless therer is no phase transition in bulk there is no change in he edge state so the edge states are topologically protected by the bulk and these edge states are robust.

It is to be noted that chiral edge state breaks time reversal symmetry. As edge current flowing left or right direction is different. So in conclusion IQH demands to break time revarsal symmetry.

Can we realize IQE with out magnetic field???.

Lets go back and discuss a bit about toy model by haldane og Graphene. Because these has led letter a clear answer of the above question. Realizing quantum hall effect without magnetic field and landau level.These are known now to be as Chern insulator/ Qunatum anomalous hall effect/ Time reversal inverient topological insulator.

The inversion symmetry can be broken by replacing graphene and B site by dissimilar atom e.g Boron nitride.

Now the time reversal symmetry with out breaking any other internal symmetry ,can be broken by considering a NNN hopping

The second nearest neighbor hopping are described in above figure by dotted line. Such hopping can be clockwise and anti clockwise and they are not equivalent !! So time reversal symmetry is broken.

Now by the above mentioned two method a gap is opened then now an interesting concepts come that is "chirality".

When a gap is open then the Dirac equation has a mass term. Now introduction of mass term give rise to chirality i,e handeness. When gap is opened by breaking the space inversion symmetry then the two Dirac point are still connected by time reversal symmetry (it basically reverse the handiness) and the net chirality is zero. But when gap is opened by breaking time inversion symmetry, then the dirac ppint preserve space inversion symmetry and the handiness is preserved. So this situation is really special.

Now let's hink about the edge when a gap is opened . Now Graphene has interesting particle hole symmetry. Because of this there is exact zero energy edge state. This zero energy state connect the two Dirac points of of graphene from bulk to the edge.

This edge state appear because of excess number either A or B site at the edge of graphene. Because of particle- hole symmetry the system require an equal number of A and B sites. Now when on the edge there is excess of any local site then it will give rise to such zero energy edge state.

Now when the gap is open the edge states has to be connected among the valence or conduction band of the Dirac cone

Now the breaking inversion symmetry make these edge state connected either with in the valence and conduction band. This case is trivial.But for broken time reversal symmetry an special situation appear when the edge connect in between valence and conduction band. This is a nontrivial case.

For graphene it is semimetal and valvce, conduction band touches at Dirac point. If we break inversion /Time reversal symmetry then a gap is opened.

Yes we can by spin orbit coupling (SOC). The SOC can give rise an fictitious magnetic field in side a material and give rise a landau level.So the system is time reversal inverient unlike IQE system!!
If we consider 2 copies of quantum hall system 1 with spin up-field and another spin down-field down and combine them together now total hall conductance is zero. But the whole system is time reversal. Then what is other way out??

These class of material known as Quantum hall insulator.

Under SOC the up and spin down will fill different force (SOC give velocity dependent transport i.e two spin Chanel ) and time reversal symmetry is conserve by kramers theorem (T^2=-1) !!. Theoretically predicted Phys. Rev. Lett. 95, 226801 (2005).

Phys. Rev. Lett. 96, 106802 (2006)

Phys. Rev. Lett. 95, 136602 (2005)

Experimentally observed by Konig et al. Science 02 Nov 2007:Vol. 318, Issue 5851, pp. 766-770 !!

So what we got is the interior is insulator but surface is conducting. It is a 2D topological insulator.

Now the question is can we have a topological insulator???

2D electron gas under magnetic field: formation of landau level

Let us consider a free electron gas assuming it as a simple charge particle with no other internal degree of freedom (e.g spin etc) in 2D dimension under magnetic field along z direction.

According to classical mechanics the electron will perform Larmor precession with cyclotron frequency ()does not depend on radius and give a special characteristic time to this problem.

But solving the problem through Quantum mechanics gives an interesting result:
The quantum Hamiltonian is H= 1/2m(P+eA/C)^2= Q.Q/2m ....(eq1)

Just to be carefull the total momentum has two contribution, one is mechanical origin another is cannonical and it is from the magnetic field (C kitel book page no. 246)

now poison bracket of different component of mechanical moment does not commute with each other e.g
{mx_i ,mx_j}=-e A_ijk B_k A_ijk is levicivita symbol
this finally give

{Q_x, Q_y}=-iehB

Now there is twist in the story , we introduce a set of new variable namly quantm mehanical eaising and lowering operator a and a' and these can be written interms of Q_x and Q_Y as following
a=1/sqrt(ehB)(Q_x-iQ_y)

a'=1/sqrt(ehB)(Q_x+iQ_y)

So now hamiltonian H=Q.Q/2m=C(aa'+1/2) where C=heB/m

Waooo..!! now the hamiltonian looks like a harmonic oscillator

So energy of nth state is E_n=(n+1/2)hw is quantize, equispaced and these level are called Landau level. Each of these level are highly degenerate.

In the above figure x axis is density of states.

So what we got is an incredible strong point and is starting to make CMP more interesting !!

If we do an experiment where quantum mechanics work i.e, low temperature and we switched a magnetic field then electron are able to occupy the state only in landau level. If we now can manipulate to move the Fermi energy E_f then if it is in between levels where no state is available then the 2D free electron gas will be behave like an insulator !! Remember these are different from the band insulator where Fermi level lie in between valence and conduction band.
* From now onwards these phase of material i.e a 2D electron gas with high magnetic field and having such beautiful Lanadau level will be called as "Landau Phase"

Integer Quantum Hall Effect:
Let's measure the transport property in Landau phase. For that we have apply an electric field with in the x-y plane let say along x direction E_y and remember magnetic field is already applied in z direction.

Now we can measure the resistivity along x direction or in y direction. Such measurement is known as Hall measurement. Whenn electric field is applied alonf x direction and resistivity is also measuring along x then the resistivity is called longitudinal R_xx and when it is along y it is called transverse R_xy.

The above figure show the experimental result. Where R_xy show discrete steps !! This is known as integer quantum hall effect. For this discovery Klitzing got nobel prize in 1985 https://www.nobelprize.org/nobel_prizes/physics/laureates/1985/klitzing.pdf .

In classical picture e.g at high temperature when so called Landau phase is not there, this should be a st line instead of discrete jump.

Explaining integar quantum hall effect through topology:

One spectacular phenomena about this quantized hall resistance is that they extremely robust with respect to sample quality, defect, geometry etc. Another important aspect is this effect is highly accurate e.g R_xy has been measured to 1 part in 10^9 !!

The hall resistivity is expressed as

R_xy=ne^2/h

Now TKNN show that this integar n can be written as

Where c/n is called Chern number, it is the total Berry flux in the Brillouin zone. Chern number c/n is a topological invariant in the sense that it cannot change when the Hamiltonian varies smoothly. This helps to explain the robust quantization of R_xy.

The Thouless-Kohmoto-Nightingale-den Nijs (TKNN) formula relates the topological invariant called the Chern number with the Hall conductivity.Topology plays an intriguing role in quantum physics under the name of the Berry phase (Rev. Mod. Phys. 82, 1959)

.The TKNN formula tells us that the Hall conductivity is proportional to the Berry phase of a closed path encompassing the entire Brillouin zone.The integer in IQE hall effect is measuring something really special i.e topological inverient. The topology of valance band as function of momentum globally could be imagined as some sort hole in different objects.

2D surfaces can be topologically classified by their genus g, which counts the number of holes. For instance, a sphere or drinking glass has g=0, while a donut/ tea cup has g=1. A theorem in mathematics due to Gauss and Bonnet (Nakahara, 1990) states that the integral of the Gaussian curvature over a closed surface is a quantized topological invariant, and its value is related to g. The Chern number is an integral of a related curvature.

The longitudinal resistance becomes zero since all electrons can flow freely at the edge of system without any back-scattering. .The edge state is protected since it is the boundary between two phases, i.e., inside and outside the system, with different topological numbers.

I left my Girl friend bcz I Love Topology !! :-)

Pages