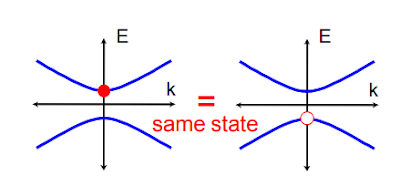
Particle hole symmetry is one of the remarkable conclusion of BCS theory.Superconductor similar to insulator in the the sense they have energy gap between the quasiparticle excitation. Now for superconductor there is intrinsic symmetry that valence and conduction are exactly mirror image of each other. But for insulator those are different. Adding an electron in conduction band is equivalent to electron from valence bond. Now for insulator these two case are independent as the valence and conduction band are independent of each other. In superconductor these states are actually same states !! In case of superconductor, For superconductor creating an particle at +E and destroying a particle at -E are in same state. This known as particle hole symmetry.
Now a question is , Does a Hamiltonian (antiunitary) that satisfy particle hole symmetry have a topological class. If yes then that would be a topological superconductor !!
In 1D there is possibility of Z2 topological superconductor. These Topological superconductor end host Majorana fermions at the edge with zero mode.
In 2D, we will have chiral majorana edge states which are protected as integer quantum hall state. But here because of particle hole symmetry the chiral state with positive and negative are redundant
here time reversal symmetry is broken and it ins Z(n) topological insulator as any integer number (n) of chiral state are possible not Z2 as in case of 1D .It is possible to observe majorana zero mode at the vortex of 2D topological superconductor.
CuxBi2Se3theory
Now what about 3D. from the following periodic table
By Kiataev and in PRB
Classification of topological insulators and superconductors in three spatial dimensions
The DIII could host a 3D topological superconductor.The quasiparticles on the surface of a
3D topological insulator are massless Dirac
fermions, familiar from graphene. The
superconducting counterpart has massless
Majorana fermions on its surface



No comments:
Post a Comment